|
 
|
Stranica: 15/17.
|
[ 423 post(ov)a ] |
|
| Autor/ica |
Poruka |
|
zaba1111
|
Naslov: Re: Matematika  Postano: Postano: 21 sij 2017, 18:37 |
|
Pridružen/a: 07 svi 2009, 13:41
Postovi: 6479
|
|
Zna li netko ima li kakva formula ili funkcija na digitronu za dobivenja rezultatnte pri slaganja silia, znači umjesto crtanja paralelograma da samo upišem intezitet sila i kut između njih i da dobijem rješenje?
Znam izračunati na XY osi sa razlaganjem, ali to uzima puno vremena, znači ima li šta efikasnije?
|
|
| Vrh |
|
 |
|
Robbie MO
|
Naslov: Re: Matematika  Postano: Postano: 21 sij 2017, 23:33 |
|
Pridružen/a: 03 svi 2009, 10:29
Postovi: 79572
Lokacija: Institut za razna i ostala pitanja
|
zaba1111 je napisao/la: Zna li netko ima li kakva formula ili funkcija na digitronu za dobivenja rezultatnte pri slaganja silia, znači umjesto crtanja paralelograma da samo upišem intezitet sila i kut između njih i da dobijem rješenje?
Znam izračunati na XY osi sa razlaganjem, ali to uzima puno vremena, znači ima li šta efikasnije? Prva sila (a), druga sila (b) i rezultanta (c) tvore trokut stranica a,b,c i kuta gama izmedju prve i druge sile. Formula koju trazis je kosinusov teorem: https://hr.wikipedia.org/wiki/Kosinusni_pou%C4%8DakTreca formula u clanku, za c kvadrat. Samo izvaditi korijen iz c. Ali moras pazit sta ubacujes za kut. Nacrtati tako da strelica prvog vektora bude AC, a strelica drugog vektora CB (prvi vektor zavrsava u C, a drugi pocinje iz C), inace ce ti se prividjeti krivi kut.
_________________
Nema Izbornog zakona BiH ako nema BiH.
Nema ukradenog hrvatskog člana Predsjedništva BiH, ako nema BiH.
33% dionica firme koja je bankrotirala vrijede 0.
Bošnjaci imaju snagu Miki Mausa.
|
|
| Vrh |
|
 |
|
zaba1111
|
Naslov: Re: Matematika  Postano: Postano: 22 sij 2017, 10:09 |
|
Pridružen/a: 07 svi 2009, 13:41
Postovi: 6479
|
|
Svaka čast, zahvaljujem, vjerujem da sam dobio točan rezultat.
Znači samo treba u formulu ubaciti vanjski kut.
Evo da potvrdimo na primjeru:
F1=60N
F2=40N
kut=50
Po formuli c2 = a2 + b2 – 2ab cos γ , bi bilo ovako:
R=korijen (3600+1600)-(2x40x60)cos130(vanjski kut)=91,02N
Što se tiče pravca sile, uz pomoć proporcija sam dobio kut od 20 stupnjeva u odnosu na silu F1.
Ima li neka formula i za kut rezultante, mada ni sa proprcijama nije vremenski zahtjevno, ukoliko je ova računica ispravna, znači da R i F1 prave kut od 20 stupnjeva.
Pa onda ako imate volje idemo dalje na primjenju fiziku iz svakodnevne prakse.
|
|
| Vrh |
|
 |
|
Robbie MO
|
Naslov: Re: Matematika  Postano: Postano: 22 sij 2017, 10:21 |
|
Pridružen/a: 03 svi 2009, 10:29
Postovi: 79572
Lokacija: Institut za razna i ostala pitanja
|
Nakon sto si izracunao rezultantu, imas situaciju da su ti poznate sve tri stranice trokuta, te jedan kut. Odatle ima par mogucih puteva za naci preostala dva kuta. Jedan je opet primjena kosinusovog poucka, ali koristeci prvu ili drugu formulu gdje je alfa ili beta jedina nepoznanica: https://hr.wikipedia.org/wiki/Kosinusni_pou%C4%8DakMozes ici i sa sinusnim pouckom: https://hr.wikipedia.org/wiki/Sinusni_pou%C4%8Dakkoji povezuje dvije stranice i dva kuta. Jedan od kuteva odaberes da bude taj kut koji je vec poznat.
_________________
Nema Izbornog zakona BiH ako nema BiH.
Nema ukradenog hrvatskog člana Predsjedništva BiH, ako nema BiH.
33% dionica firme koja je bankrotirala vrijede 0.
Bošnjaci imaju snagu Miki Mausa.
|
|
| Vrh |
|
 |
|
zaba1111
|
Naslov: Re: Matematika  Postano: Postano: 22 sij 2017, 10:44 |
|
Pridružen/a: 07 svi 2009, 13:41
Postovi: 6479
|
|
To ipak zahtjeva više vremena od porporcije ukoliko proporcija funkcionira?
Mada mi nije jasno ni kako bi dobio pravac rezultante uz pomoć ovih formula jer pravac rezultante je između pravaca b i c, što se najlakše vidi crtanjem paralelograma.
|
|
| Vrh |
|
 |
|
Robbie MO
|
Naslov: Re: Matematika  Postano: Postano: 22 sij 2017, 10:48 |
|
Pridružen/a: 03 svi 2009, 10:29
Postovi: 79572
Lokacija: Institut za razna i ostala pitanja
|
|
Pravac (mislis smjer?) u odnosu na sto?
Stavi sliku.
_________________
Nema Izbornog zakona BiH ako nema BiH.
Nema ukradenog hrvatskog člana Predsjedništva BiH, ako nema BiH.
33% dionica firme koja je bankrotirala vrijede 0.
Bošnjaci imaju snagu Miki Mausa.
|
|
| Vrh |
|
 |
|
zaba1111
|
Naslov: Re: Matematika  Postano: Postano: 22 sij 2017, 11:23 |
|
Pridružen/a: 07 svi 2009, 13:41
Postovi: 6479
|
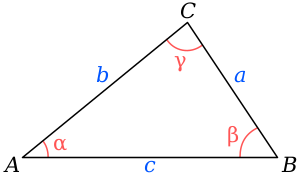 Znači kut alfa se traži, ove formule bi trebalo sabrati i izvući alfu, skonto sam sad, pokušat ču to napraviti c^{2}=a^{2}+b^{2}-2ab\cos \gamma \ a^{2}=b^{2}+c^{2}-2bc\cos \alpha \,
|
|
| Vrh |
|
 |
|
zaba1111
|
Naslov: Re: Matematika  Postano: Postano: 22 sij 2017, 11:26 |
|
Pridružen/a: 07 svi 2009, 13:41
Postovi: 6479
|
|
Da ne kompliciramo:
F1=60N
F2=40N
kut=50
koji kut ce biti između rezultante i F1
I kako doći do toga kuta.
|
|
| Vrh |
|
 |
|
zaba1111
|
Naslov: Re: Matematika  Postano: Postano: 22 sij 2017, 13:31 |
|
Pridružen/a: 07 svi 2009, 13:41
Postovi: 6479
|
|
došao sam do formule:
sin(alfa)=a sin(gama) / c
I stao na tome da iz izračunate desne strane ne znam doći do alfe.
|
|
| Vrh |
|
 |
|
zaba1111
|
Naslov: Re: Matematika  Postano: Postano: 22 sij 2017, 18:33 |
|
Pridružen/a: 07 svi 2009, 13:41
Postovi: 6479
|
|
Uglavnom robiju zahvaljujem, stvari su mi jasnije, a kako doći do ovoga kuta alfa još uvijek ne znam, ali sam našao aplikaciju koja jednostavno rješava sve , samo se upišu sile i kut i ona izbaci i rezultantu i kut.
Sad ću postaviti ozbiljnije pitanje.
Ako uronimo žlicu u med, gdje je drška slobodna, a radni dio je uronjen, centar mase pri gibanju sada postaje nebitan, a otpor pruža med samo na području radnog dijela pa nas sada interesira centar otpora, koji će logično biti na sredini uronjenog dijela, pošto silom možemo djelovati samo na dršku, djelovanjem single sile u horizontalnom smjeru žlica će rotirati oko centra rotacije, pitanje je gdje se nalazi centar rotacije? poklapa se sa centrom optpora , nalazi se na sredini dužine između Centra otpora i donjeg dijela žlice ili na nekom trećem mjestu?
i Drugo pitanje, može li se promjenom hvatišta sile duž drške , mijenjati centar rotacije, odnosno možemo li uopće single silom ,na dršku koja nije uronjena, mijenjati centar rotacije(smjer sile je horizintalan)
|
|
| Vrh |
|
 |
|
Robbie MO
|
Naslov: Re: Matematika  Postano: Postano: 22 sij 2017, 21:03 |
|
Pridružen/a: 03 svi 2009, 10:29
Postovi: 79572
Lokacija: Institut za razna i ostala pitanja
|
Kada dodjes do Sin(Alpha) = neki broj Treba ti inverzna funkcija za sinus (ono sto je korijen za kvadrat). Ta funkcija se zove arkus sinus (Arcsin) i na kalkulatoru je obično označena sa Sinus na minus prvu potenciju (Sin-1). Znaci rješenje će ti biti Alpha = Sin-1 (neki broj) Inače taj -1 nema veze s potenciranjem, to je ukras, samo konvencija kako označiti inverznu funkciju. Da ne bi išao dizati na -1 potenciju.  Ako imaš aplikaciju, još bolje, ali nije loše razumjeti malo trigonometrije.
_________________
Nema Izbornog zakona BiH ako nema BiH.
Nema ukradenog hrvatskog člana Predsjedništva BiH, ako nema BiH.
33% dionica firme koja je bankrotirala vrijede 0.
Bošnjaci imaju snagu Miki Mausa.
|
|
| Vrh |
|
 |
|
Robbie MO
|
Naslov: Re: Matematika  Postano: Postano: 22 sij 2017, 21:11 |
|
Pridružen/a: 03 svi 2009, 10:29
Postovi: 79572
Lokacija: Institut za razna i ostala pitanja
|
zaba1111 je napisao/la: Uglavnom robiju zahvaljujem, stvari su mi jasnije, a kako doći do ovoga kuta alfa još uvijek ne znam, ali sam našao aplikaciju koja jednostavno rješava sve , samo se upišu sile i kut i ona izbaci i rezultantu i kut.
Sad ću postaviti ozbiljnije pitanje.
Ako uronimo žlicu u med, gdje je drška slobodna, a radni dio je uronjen, centar mase pri gibanju sada postaje nebitan, a otpor pruža med samo na području radnog dijela pa nas sada interesira centar otpora, koji će logično biti na sredini uronjenog dijela, pošto silom možemo djelovati samo na dršku, djelovanjem single sile u horizontalnom smjeru žlica će rotirati oko centra rotacije, pitanje je gdje se nalazi centar rotacije? poklapa se sa centrom optpora , nalazi se na sredini dužine između Centra otpora i donjeg dijela žlice ili na nekom trećem mjestu?
i Drugo pitanje, može li se promjenom hvatišta sile duž drške , mijenjati centar rotacije, odnosno možemo li uopće single silom ,na dršku koja nije uronjena, mijenjati centar rotacije(smjer sile je horizintalan) Ne mogu preko mobitela. 
_________________
Nema Izbornog zakona BiH ako nema BiH.
Nema ukradenog hrvatskog člana Predsjedništva BiH, ako nema BiH.
33% dionica firme koja je bankrotirala vrijede 0.
Bošnjaci imaju snagu Miki Mausa.
|
|
| Vrh |
|
 |
|
Robbie MO
|
Naslov: Re: Matematika  Postano: Postano: 23 sij 2017, 01:11 |
|
Pridružen/a: 03 svi 2009, 10:29
Postovi: 79572
Lokacija: Institut za razna i ostala pitanja
|
Pretpostavljam da je med dovoljno gust da se zlica moze "zabosti" u med i da "ne tone" ili jako sporo tone, ili ju se pak pridrzava da nema vertikalno gibanje? Ovaj problem nije tako trivijalan, ako ga mislis bas tocno rijesiti, koristeci minimalne aproksimacije. Npr. "ugrubo" se moze pretpostaviti da sila otpora djeluje negdje pri sredini uronjenog dijela, i dobit ces nekakav rezultat, ali moze se to puno bolje. Ja bih prvo krenuo razmotriti par jednostavnijih situacija gdje se jasno moze vidjeti kako sto funkcionira, pa bih ih onda krenuo sklapati prema tom problemu kao konacnoj situaciji koja je malo kompleksnija. Ako hoces dobro izracunati, mislim da stvari nisu tako jednostavne kako si pretpostavio. Idemo redom. 1) "Centar otpora".Mislim da nije bas na sredini uronjenog dijela, iako ocito jest negdje izmedju dva kraja uronjenog dijela. S obzirom da se zlica giba kroz med ovo sto zoves "otpor" zapravo je sila viskoznosti (neka vrsta otpora ili trnja pri kretanju kroz materijal). Pri malim brzinama kretanja kroz viskozni materijal, sila viskoznosti je proporcionalna brzini kretanja kroz materijal. Recimo ako imas malenu kuglu koja se sporo giba brzinom v kroz tekucinu viskoznosti ETA , silu otpora opisuje Stokesov zakon: https://en.wikipedia.org/wiki/Stokes'_lawOvaj zakon vrijedi samo za kuglu i samo za malene brzine, ali glavna poanta je da je sila otpora pri kretanju kroz sredstvo (pri malim brzinama) proporcionana brzini kretanja. E sad zamisli jednostavniju situaciju od te tvoje: rotaciju oko tocke A (slika dolje). Znaci zamisli da je donji kraj debelog stapa (radije zamisljam stap nego zlicu), pricvrscen u tocki A (fiksirana os), tako da je stap prisiljen rotirati oko tocke A. Ovo naravno nije tvoj problem ali je jednostavniji problem gdje se vidi kako viskoznost na stap radi. Jasno je da dijelovi stapa koji su dalje od tocke A se gibaju brze kroz med, tako da ce (prema Stokesovom zakonu), imati i jaci otpor. Med se opire gibanju predmeta, i sila otpora je suprotnog smjera od smjera gibanja. Otpor ce najmanji biti oko tocke A, gdje ce biti nula. Ne mijesati ovaj otpor viskoznosti (sto je nista drugo nego trenje tekucine), sa silom reakcije koju daje lezaj u tocki A, koji pridrzava stap. Sila otpora viskoznosti raste od 0 u tocki A do neke vrijednosti u tocki B. Linearan je rast jer brzina tocaka na stapu raste linearno s udaljenoscu od A, pri rotaciji oko A. Tocke koje su dalje od A imaju vecu "tezinu" pri odredjivanju gdje je "centar otpora". Isto tako centar otpora ovisi o tocki oko koje stap rotira. Za slucaj prisiljenog rotiranja oko tocke A, mislim da se uz malo integracije moze pokazati da se "centar otpora" nalazi na 2/3 udaljenosti |AB|, gledano od tocke A (to pogadjam jer se teziste trokuta kojeg prave ove strelice otpora, nalazi na 2/3 visine). Ovo je samo da te uvjerim da nije bas tako jednostavno da se moze uzeti da med daje otpor na sredini uronjenog dijela. To bi bilo tako da su sve točke na štapu izložene jednakom otporu, ali nisu. Gdje je ta tocka gdje bi se moglo reci da ukupni otpor djeluje, ovisi o centru rotacije jer on utječe na raspodjelu brzina kojima se razne točke štapa krecu. Centar rotacije u tvom slucaju nece biti tocka A (treba ga tek pronaći, nadam se uz par jednadžbi). Dovoljno za danas. Kasnije mozemo olabaviti pretpostavke i pogledati sto se dogadja kada stap nije ucvrscen u A, nego slobodan.
| Privitak/ci: |

med0.png [ 4.52 KiB | Pogledano 7149 put/a. ]
|
_________________
Nema Izbornog zakona BiH ako nema BiH.
Nema ukradenog hrvatskog člana Predsjedništva BiH, ako nema BiH.
33% dionica firme koja je bankrotirala vrijede 0.
Bošnjaci imaju snagu Miki Mausa.
|
|
| Vrh |
|
 |
|
zaba1111
|
Naslov: Re: Matematika  Postano: Postano: 23 sij 2017, 10:02 |
|
Pridružen/a: 07 svi 2009, 13:41
Postovi: 6479
|
|
Sa razlicitim otporom pri ralizlicitoj brzini je postalo prilicno komplicirano, pa da pojednostavimo, a to je ono sto me i interesira, predpostavimo da je otpor konstantan jer je sila toliko blaga da ona tek moze savladati viskoznost i da je time brzina jako mala, recimo da ce se stap u tocki B pomaknuti za jedan cm kroz mjesec dana.
Sto se tice centra otpora, nije mi jasno kako moze biti igdje drugo osim na sredini uronjenog dijela stapa ukoliko je stap pravilnkog oblika, osim ako je viskoznost manja na povrsini, ali u tom slucaju idemo u previse komplikacija koje nisu potrebne.
Sto se tice centra rotacije , jasno mi je da bi se poklapao sa centrom otpora ukoliko bi imali spreg sila, medjutim ovdje imamo jednu silu na jednom kraku , gdje logika govori da bi Cr trebao biti izmedju Co i dna stapa, ali ipak , ao sto kazes, stvari nisu tako jednostavne.
|
|
| Vrh |
|
 |
|
Robbie MO
|
Naslov: Re: Matematika  Postano: Postano: 23 sij 2017, 14:01 |
|
Pridružen/a: 03 svi 2009, 10:29
Postovi: 79572
Lokacija: Institut za razna i ostala pitanja
|
|
Ok, idemo pretpostaviti pojednostavljeno da sila otpora sva djeluje na sredini uronjenog dijela. Tocnost krajnjeg rezultata ovisit ce o tocnosti ove pretpostavke.
To znaci da na stap djeluju dvije sile:
-Sila F, u tocki C, prema lijevo.
-Sila nazovimo ju N, u tocki na pola puta izmedju A i B, djeluje prema desno.
Sada jedna vazna pretpostavka:
Mozemo pretpostaviti da je viskoznost toliko velika da ubrzo nakon pocetka djelovanja sile stap uspostavlja konstantnu brzinu gibanja (ili rotiranja). Ovo je slicna situacija pri otvaranju padobrana: nedugo nakon sto se padobran otvori (smisao padobrana je da osigura otpor zraka) skakac postize konstantnu brzinu padanja (tzv. kriticna brzina).
E sad, s obzirom da se stap giba prema lijevo (plus rotira suprotno od kazaljke sata) konstantnom brzinom, slijedi da je akceleracija stapa nula. To znaci da prema drugom Newtonovom zakonu (totalna sila na stap = masa * akceleracija) , ako je akceleracija 0 slijedi da ukupna sila na stap mora biti 0.
Kako imamo samo dvije sile a ukupna mora biti 0, to znaci da je ova sila otpora po iznosu tocno jednaka sili guranja F.
To ima smisla. Kada se zlica tek pocinje gurati, ona inicijalno ima brzinu 0, i povecava brzinu (cime se povecava i sila viskoznosti N) sve dok se N ne izjednaci sa F. (slicno situaciji kada padobranac s otvorenim padobranom usporava sve dok se sila otpora zraka ne izjednaci s gravitacijom. Nakon sto se izjednace, pada konstantnom brzinom.)
Znaci prakticki smo rijesili iznos sile otpora. Jednostavno, N=F. Na tijelo koje se giba jednolicno (ne ubrzava) ukupna sila mora biti nula.
I sada imas samo problem gibanja krutog tijela kada djelujes na njega silom F u tocki C prema lijevo, i silom istog iznosa (F) u tocki na pola puta izmedju A i B, koja djeluje prema desno.
Te dvije sile stvaraju spreg sila (moment).
Centar rotacije ce biti na pola puta izmedju hvatista ove dvije sile, odnosno u sredini izmedju tocke C i tocke koja je na pola puta A-B.
_________________
Nema Izbornog zakona BiH ako nema BiH.
Nema ukradenog hrvatskog člana Predsjedništva BiH, ako nema BiH.
33% dionica firme koja je bankrotirala vrijede 0.
Bošnjaci imaju snagu Miki Mausa.
|
|
| Vrh |
|
 |
|
Robbie MO
|
Naslov: Re: Matematika  Postano: Postano: 23 sij 2017, 14:39 |
|
Pridružen/a: 03 svi 2009, 10:29
Postovi: 79572
Lokacija: Institut za razna i ostala pitanja
|
Osim rotacije oko te tocke postoji i translacija (gibanje samog centra rotacije) prema lijevo. E sad, za promatraca iz vana, tijelo koje rotira i giba se, moze se "ciniti" da rotira oko druge tocke, zbog efekta tzv. "trenutnog centra rotacije". Npr. kada imas kotac koji se kotrlja bez prolizavanja, njegovo ukupno gibanje se moze predstaviti kao rotacija oko centra kotaca + gibanje tog centra. No, isto tako se gibanje tog kotaca, u tom promatranom trenutku, moze predstaviti kao cista rotacija bez translacije, oko jedne druge tocke, a to je tocka u kojoj kotac dodiruje pod. http://physics.info/rolling/http://www.wikiwand.com/en/Instant_centre_of_rotationRastav gibanja tijela na rotaciju i translaciju (promatrajuci samo trenutak) nije jedinstven.
_________________
Nema Izbornog zakona BiH ako nema BiH.
Nema ukradenog hrvatskog člana Predsjedništva BiH, ako nema BiH.
33% dionica firme koja je bankrotirala vrijede 0.
Bošnjaci imaju snagu Miki Mausa.
|
|
| Vrh |
|
 |
|
KiM
|
Naslov: Re: Matematika  Postano: Postano: 23 sij 2017, 14:48 |
|
Pridružen/a: 10 lip 2015, 23:16
Postovi: 6001
|
|
Robbie jesi li ti znanstvenik ?
_________________
Kako smo svi opljackani.Film "Tezina lanaca" https://youtu.be/waEYQ46gH08
Film o propasti imperije duge 1.123 g. Vizantijska lekcija https://youtu.be/_fLuI92iHR4
|
|
| Vrh |
|
 |
|
Robbie MO
|
Naslov: Re: Matematika  Postano: Postano: 23 sij 2017, 14:49 |
|
Pridružen/a: 03 svi 2009, 10:29
Postovi: 79572
Lokacija: Institut za razna i ostala pitanja
|
|
Ne.
Ovo je sve srednjoskolska matematika i fizika.
_________________
Nema Izbornog zakona BiH ako nema BiH.
Nema ukradenog hrvatskog člana Predsjedništva BiH, ako nema BiH.
33% dionica firme koja je bankrotirala vrijede 0.
Bošnjaci imaju snagu Miki Mausa.
|
|
| Vrh |
|
 |
|
KiM
|
Naslov: Re: Matematika  Postano: Postano: 23 sij 2017, 14:55 |
|
Pridružen/a: 10 lip 2015, 23:16
Postovi: 6001
|
|
Vidim lepo se razumeš u matematiku fiziku. Možda kao hobi prirodne nauke ti leže.
_________________
Kako smo svi opljackani.Film "Tezina lanaca" https://youtu.be/waEYQ46gH08
Film o propasti imperije duge 1.123 g. Vizantijska lekcija https://youtu.be/_fLuI92iHR4
|
|
| Vrh |
|
 |
|
Robbie MO
|
Naslov: Re: Matematika  Postano: Postano: 23 sij 2017, 14:57 |
|
Pridružen/a: 03 svi 2009, 10:29
Postovi: 79572
Lokacija: Institut za razna i ostala pitanja
|
Razumijem se pomalo u razne stvari i imam veliku privatnu biblioteku  , medjutim nemaju tajna vrata. Staromodni renesansni čovjek. 
_________________
Nema Izbornog zakona BiH ako nema BiH.
Nema ukradenog hrvatskog člana Predsjedništva BiH, ako nema BiH.
33% dionica firme koja je bankrotirala vrijede 0.
Bošnjaci imaju snagu Miki Mausa.
|
|
| Vrh |
|
 |
|
KiM
|
Naslov: Re: Matematika  Postano: Postano: 23 sij 2017, 15:11 |
|
Pridružen/a: 10 lip 2015, 23:16
Postovi: 6001
|
|
Kada se oženiš i dodju djeca i jače obaveze malo ćeš pozaboravljati. Jedino ako uzmeš ženu sličnih performansi pa se nadogradjujete i nadopunjujete zajedno.
_________________
Kako smo svi opljackani.Film "Tezina lanaca" https://youtu.be/waEYQ46gH08
Film o propasti imperije duge 1.123 g. Vizantijska lekcija https://youtu.be/_fLuI92iHR4
|
|
| Vrh |
|
 |
|
zaba1111
|
Naslov: Re: Matematika  Postano: Postano: 23 sij 2017, 16:23 |
|
Pridružen/a: 07 svi 2009, 13:41
Postovi: 6479
|
|
Nismo se razumjeli, kad kazem Centar otpora onda mislim na tocku kroz koju kad djeluje sila tijelo se giba translatorno, bez ikakve rotacije. Znaci sila sa tvoje slike tu ne igra ulogu jer je ta tocka nepronjenjljiva dok je god jednaka kolicina stapa uronjena, a to ne smijemo mijenjati ili barem predpostavimo da bi pri laganom izvlecenju , zbog ljepljivosti meda , stap povukao med za sobom i time bi polje otpora ostalo isto.
Sila sa tvoje slike djeluje na slobodni dio stapa i uzrokuje rotaciju tijela oko centra rotacije, koji se ne poklapa sa centrom otpora, a centar rotacije je promjenjljiv, znaci pitanje s pocetka je gdje je taj centar rotacije na tvojoj slici, i ako je moguce tu poziciju Cr objasniti.
A kasnije cemo doci do toga kako mjenjati, slaganjem sila i raznim polugama , centar rotacije i njime upravljati po zelji kako bi dobili razlicita gibanja.
|
|
| Vrh |
|
 |
|
Robbie MO
|
Naslov: Re: Matematika  Postano: Postano: 23 sij 2017, 17:06 |
|
Pridružen/a: 03 svi 2009, 10:29
Postovi: 79572
Lokacija: Institut za razna i ostala pitanja
|
zaba1111 je napisao/la: Nismo se razumjeli, kad kazem Centar otpora onda mislim na tocku kroz koju kad djeluje sila tijelo se giba translatorno, bez ikakve rotacije. Znaci sila sa tvoje slike tu ne igra ulogu jer je ta tocka nepronjenjljiva dok je god jednaka kolicina stapa uronjena, a to ne smijemo mijenjati ili barem predpostavimo da bi pri laganom izvlecenju , zbog ljepljivosti meda , stap povukao med za sobom i time bi polje otpora ostalo isto.
Sila sa tvoje slike djeluje na slobodni dio stapa i uzrokuje rotaciju tijela oko centra rotacije, koji se ne poklapa sa centrom otpora, a centar rotacije je promjenjljiv, znaci pitanje s pocetka je gdje je taj centar rotacije na tvojoj slici, i ako je moguce tu poziciju Cr objasniti.
A kasnije cemo doci do toga kako mjenjati, slaganjem sila i raznim polugama , centar rotacije i njime upravljati po zelji kako bi dobili razlicita gibanja. Zbunjujes me sada. Ajmo nazad na pocetak, sto ti predstavlja tocka koju zoves "centar otpora"? Jer, u prvom postu si rekao "uzmimo da je centar otpora tocka koja se nalazi na sredini uronjenog dijela", iz cega sam ja shvatio da zelis silu viskoznosti, koja se zapravo sastoji od puno malih sila od kojih svaka djeluje na djelic uronjenog stapa, zamijeniti s jednom silom koja bi po iznosu bila jednaka sumi svih tih malih sila, a imala bi hvatiste u sredistu uronjenog dijela. No sada u zadnjem postu si drugacije definirao "centar otpora". Kako sam ja shvatio, tu si rekao da zelis naci tocku takvu da kad na tijelo djeluje sila (mislis na silu F?) bas u toj tocki, da se tijelo giba translatorno i da nema rotacije. Ako nema nikakve rotacije, odnosno tijelo se giba translatorno, ukupni moment (spreg sila) mora biti nula. Jedan nacin da se to postigne je sa F djelujes u istom hvatistu gdje si pretpostavio da je i "hvatiste" sile otpora, samo suprotnog smjera. Znaci pod vodom, odnosno medom. Mislim da je to ujedno i jedini nacin, pogotovo ako pretpostavimo da stap ne ubrzava translatorno, nego se giba konstantnom translatornom brzinom, sto znaci da ukupna sila na stap mora biti nula, sto znaci da je sila otpora po iznosu jednaka sili guranja/vucenja F. Generalno, ima vise odgovora na pitanje "kada masivni stap nece rotirati (cista translacija)" kada na njega djeluju dvije okomite sile? Dolje sam nacrtao dvije situacije. U prvom slucaju dvije sile od 5N i 10N, u drugom slucaju obje sile 10N. Ukupni moment oko centra stapa u oba slucaja je nula. I stap nece rotirati ni u prvom ni u drugom slucaju. U prvom slucaju ce ubrzavati translatorno (jer ukupna sila nije nula), a u drugom ce ili stojati na mjestu ili se gibati konstantnom brzinom po pravcu. Medjutim ako je pretpostavka da nema translatorne akceleracije (priguseno gibanje poput padoranca), onda F i N (gdje sam sa "N" oznacio silu otpora meda, a sa "F" silu guranja stapa od strane covjeka/stroja) moraju imati isti iznos, sto znaci da moraju dijeliti isto hvatiste, inace im se momenti nece ponistavati. Znaci dolje ako pitas "Ako imas jednu silu od 10N koja djeluje na cetvrtini stapa, gdje trebas djelovati drugom silom, tako da sve skupa ne stvara moment (spreg)?" To pitanje ima vise odgovora, ovisno koliko hoces da bude jaka ta druga sila. Ali kad specificiras jakost te druge sile, onda postoji samo jedno rjesenje za hvatiste koje ponistava spreg/moment. Jasno, taj stap dolje ce ubrzavati translatorno ako ukupna sila nije nula. Ako trazis da nema ubrzanja, to fiksira drugu silu na iznos prve sile, i onda hvatiste mora biti u istoj tocki ako neces da ima rotacije.
| Privitak/ci: |

IMG_2180.JPG [ 1.31 MiB | Pogledano 7038 put/a. ]
|
_________________
Nema Izbornog zakona BiH ako nema BiH.
Nema ukradenog hrvatskog člana Predsjedništva BiH, ako nema BiH.
33% dionica firme koja je bankrotirala vrijede 0.
Bošnjaci imaju snagu Miki Mausa.
|
|
| Vrh |
|
 |
|
zaba1111
|
Naslov: Re: Matematika  Postano: Postano: 23 sij 2017, 17:23 |
|
Pridružen/a: 07 svi 2009, 13:41
Postovi: 6479
|
|
U prvom postu sam naveo centar mase, odnosno teziste , i rekao kako ono sad postaje nebitno jer je tijelo uronjeno i otpor gibanju je odredjen iskljucivo uronjenim dijelom pa stoga nam je sad umjesto centra mase znacajn centar otpora.
Dakle kad kazem centrar otpora onda mislim na tocku kroja imitira teziste u okolnostima uronjenog tijela, znaci tocka na stapu uronjenom u med , u kojoj je se pri apilakciji sile na nju dogadja cista translacija.
A ukoliko je hvatiste u bilo kojoj drugoj tocki imat cemo i moment i rotaciju, razlaganjem gibanja imat cemo i translaciju i rotaciju, osim ukoliko nemamo spreg na istoj udljenosti od centra otpora. Znaci izmedju dvije krajnosti, prolasku kroz Co i translacije i spomenutog sprega kada imamo cistu rotaciju , sve drugo je kombinacija ta dva gibanja koja ovisi o odaljenosti od centra otproa, dakle to su osnove koje su mi jasne, ali mene interesira kako manipulirati...
|
|
| Vrh |
|
 |
|
Robbie MO
|
Naslov: Re: Matematika  Postano: Postano: 23 sij 2017, 17:38 |
|
Pridružen/a: 03 svi 2009, 10:29
Postovi: 79572
Lokacija: Institut za razna i ostala pitanja
|
|
Pa ako ne zelis rotaciju, morat ces gurati posred uronjenog dijela.
Ajmo zamislit da se vozimo u gliseru.
I uronis letvu ili veslo, okomito u more. Ogromna sila otpora mora. Ako pridrzavas letvu iznad sredine uronjenog dijela, pocet ce se rotirati poput vodenice, zbog jaceg momenta mora na donji dio letve. Ako pridrzavas ispod sredine uronjenog dijela, recimo pri uronjenom dnu letve, pocet ce se prevrtati u suprotnom smjeru. Ako ne zelis da se prevrce, moras u sredini pridrzavati.
Znaci sredina ti ne gine, i ako inzistiras da nema rotacije i prevrtanja jedina manipulacija ti je uranjanje ili izranjanje letve, odnosno vertikalna pozicija.
_________________
Nema Izbornog zakona BiH ako nema BiH.
Nema ukradenog hrvatskog člana Predsjedništva BiH, ako nema BiH.
33% dionica firme koja je bankrotirala vrijede 0.
Bošnjaci imaju snagu Miki Mausa.
|
|
| Vrh |
|
 |
Online |
Trenutno korisnika/ca: / i 4 gostiju. |
|
Ne možeš započinjati nove teme.
Ne možeš odgovarati na postove.
Ne možeš uređivati svoje postove.
Ne možeš izbrisati svoje postove.
Ne možeš postati privitke.
|
|
|



 , medjutim nemaju tajna vrata.
, medjutim nemaju tajna vrata. 