|
 
|
Stranica: 13/17.
|
[ 423 post(ov)a ] |
|
| Autor/ica |
Poruka |
|
Crvena Sonja
|
Naslov: Re: Matematika  Postano: Postano: 29 svi 2014, 20:57 |
|
Pridružen/a: 11 sij 2011, 13:22
Postovi: 2985
|
 Hajde sad, ako ne znate ima guglet:D Imaš tri broja 1 ,tri broja 3 ,tri broja 5, tri broja 7 i tri broja 9. moraš uzeti 6 brojeva od tih 15 brojeva,tako da kad ih zbrojiš dobiješ broj 21.
|
|
| Vrh |
|
 |
|
Robbie MO
|
Naslov: Re: Matematika  Postano: Postano: 29 svi 2014, 23:59 |
|
Pridružen/a: 03 svi 2009, 11:29
Postovi: 81985
Lokacija: Institut za razna i ostala pitanja
|
|
Dala si na raspolaganje samo neparne brojeve.
Bilo kojih 6 neparnih brojeva kad se zbroje daju paran zbroj (isto kao i dva neparna broja, ili cetiri, itd..).
Znaci nemoguce je od tih brojeva napraviti 21.
_________________
Bošnjaci su primali 30 godina ogromnu političku pomoć, da ne liče na potpuni kurac.
Pomoć je presahla nažalost.
|
|
| Vrh |
|
 |
|
Crvena Sonja
|
Naslov: Re: Matematika  Postano: Postano: 02 lip 2014, 11:54 |
|
Pridružen/a: 11 sij 2011, 13:22
Postovi: 2985
|
|
Točno.
Neki se ubiju zbrajajući.
|
|
| Vrh |
|
 |
|
Ministry of Sound
|
Naslov: Re: Matematika  Postano: Postano: 03 lip 2014, 14:39 |
|
Pridružen/a: 03 svi 2009, 09:25
Postovi: 43757
Lokacija: Folklorni Jugoslaven, praktični Hrvat
|
|
U čast Panini albuma, evo pitanja u tom duhu.
Ako album sadrži 639 sličica, i ako Panini ne laže kada kažu da su sve sličice ravnomjerno raspoređene, koliko sličica (odnosno paketa od 5) morate kupiti da bi popunili album (dakako, kada se ne bi mogli mijenjati)?
Dalje, kada bi vam falila samo 1 sličica da popunite album, kada bi ste kupili 100 sličica (20 paketa), koja je vjerojatnoća da bi ste dobili sličicu koja vam treba?
_________________
sklon'se bona Zineta sa penđera, vidiš da te vlasi oćima kurišu

|
|
| Vrh |
|
 |
|
Leonardo Da Vinci
|
Naslov: Re: Matematika  Postano: Postano: 03 lip 2014, 22:51 |
|
Pridružen/a: 03 ruj 2009, 01:51
Postovi: 798
|
Ministry of Sound je napisao/la: U čast Panini albuma, evo pitanja u tom duhu.
Ako album sadrži 639 sličica, i ako Panini ne laže kada kažu da su sve sličice ravnomjerno raspoređene, koliko sličica (odnosno paketa od 5) morate kupiti da bi popunili album (dakako, kada se ne bi mogli mijenjati)?
Naravno, nikad ne možeš biti siguran da će se sve popuniti. Osim ako ne kupiš sve sličice na svijetu. Ali možemo približno procijeniti. Odnosno odgovoriti na pitanje: ako kupimo n sličica, koliko će sličica biti popunjeno od N=639 mjesta? Nazovimo "prosječni očekivani" broj popunjenih sličica f(n). f(n) je nepoznata funkcija koju želimo odrediti. Iz logičkog razmatranja možemo već na prvi pogled vidjeti neka njena svojstva: 1. f(n) je monotono rastuća funkcija. Što je n veći, f(n) je veći. 2. Za male n, približno je f(n)=n. Znači za male n funkcija f(n) ima linearan rast. Zašto: Ako kupimo mali broj n sličica, ne bi trebalo biti duplikata, pa očekujemo da je približno f(n)=n. 3. Za beskonačan broj kupljenih sličica, očekujemo da je cijeli album popunjen, dakle f(beskonačno)=N. Znači očekujemo da funkcija f(n) prvo raste linearno, i to s nagibom 1, i onda raste sve sporije i sporije i približava se maksimalnoj vrijednosti N=639 ali ju nikada ne dostiže. Ajmo se sada baciti na računanje f(n). Pođimo od približne rekurzivne relacije: Ako smo kupili n sličica, onda je popunjeno f(n) mjesta. Sada kupimo još jednu sličicu. Koliki je f(n+1)? f(n+1) će biti f(n) (koliko je već popunjeno) plus očekivano popunjenje zbog dodatka još jedne sličice. Ako dodamo još jednu sličicu, a pri tome je f(n) popunjeno i N-f(n) nepopunjeno, onda je šansa da ta sličica padne među ove nepopunjene jednaka postotku nepopunjenih, dakle [ N-f(n) ]/N = 1-f(n)/N. Dodatkom jedne sličice očekivani porast popunjenja je dakle 1-f(n)/N. To je neki broj manji od 1 a veći od 0. Znači možemo pisati f(n+1)=f(n)+dodatak f(n+1)=f(n)+1-f(n)/N Ovo je rekurzivna jednadžba, a one su iznimno teške za egzaktno rješavati jer ne postoji ni danas u 21. stoljeću generalna metoda za njihovo rješavanje, te se mora improvizirati i pogađati, a vrlo često i nemaju zatvorenih rješenja. Ideja je sada da pretpostavimo da je n kontinuiran broj, a ne diskretan, da bi ovo pretvorili u diferencijalnu jednadžbu. Ideja je da isforsiramo derivaciju. Prebacimo f(n) s desne strane na lijevu i pogledajmo šta dobijamo: f(n+1)-f(n)=1-f(n)/N Lijevu stranu prepoznajemo kao približno derivaciju od f; f '(n) = 1- f(n)/N. Ovo je diferencijalna jednadžba koju je lagano riješiti. Udarimo supstituciju u=1-f(n)/N, df=-Ndu i dobijamo du/dn=-u/N odnosno du/u=-dn/N Integriranjem obje strane dobijamo ln(u)+A=-n/N, gdje je A konstanta integracije koju ćemo namjestiti iz početnih uvjeta. Nakon što eksponenciramo obje strane exp[]: u=C exp (-n/N) gdje je C neka druga konstanta koju treba namjestiti. Vraćanjem nazad sa u na broj popunjenih f: 1-f/N= C exp (-n/N) dobijamo f(n)=N [1-C exp(-n/N)] Početni uvjet: Znamo da za n=0, broj popunjenih je f(n)=0, pa uvrštavanjem tog uvjeta dobijamo C=1. Konačno rješenje je f(n)=N[1-exp(-n/N)]Graf:  f(n) je crvena linija. Vidimo da se funkcija ponaša kako smo očekivali. Za male n raste linearno, a za velike usporava rast i nikad ne dostiže N. Iz grafa se vidi da se preporučuje zamjena nakon kupovine preko 1000 sličica. Ovaj graf možeš eksperimentalno verificirati tako da u određenom trenutku usporediš koliko si kupio, a koliko se popunilo.  Drugi dio pitanja mislim da možeš i sam. 
|
|
| Vrh |
|
 |
|
Leonardo Da Vinci
|
Naslov: Re: Matematika  Postano: Postano: 03 lip 2014, 22:56 |
|
Pridružen/a: 03 ruj 2009, 01:51
Postovi: 798
|
Inače možeš probati Taylorov razvoj funkcije f(n)=N[1-exp(-n/N)] za male n, te uzeti samo prva dva člana razvoja eksponencijalne funkcije. Naime vrijedi 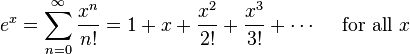 uzimanjem samo prva dva člana, N se pokrati i dobiješ f(n)=n što je upravo ono što smo očekivali za male n.
|
|
| Vrh |
|
 |
|
DzoniBG
|
Naslov: Re: Matematika  Postano: Postano: 03 lip 2014, 23:35 |
|
Pridružen/a: 28 sij 2010, 18:54
Postovi: 13005
|
Ministry of Sound je napisao/la: U čast Panini albuma, evo pitanja u tom duhu.
Ako album sadrži 639 sličica, i ako Panini ne laže kada kažu da su sve sličice ravnomjerno raspoređene, koliko sličica (odnosno paketa od 5) morate kupiti da bi popunili album (dakako, kada se ne bi mogli mijenjati)?
Kada imamo totalno prazan album, verovatnoca da ce prva slicica biti ona koju nemamo je 100%... vec druga slajba ima sansu (638/639)x100%...treca (637/639)x100%...itd... Mozemo razviti u red,prikazati preko sume, ali iz aviona se vidi da je serija harmonika, koju koriscenjem prirodnog logaritna(osnova e) mozemo aproksimirati preko jednostavne formule: ako je n je ukupan broj slicica u albumu... S= n x ln(n) = 639 x ln 639 = 4128Posto u paketu ima 5 slajbi, treba ti u proseku 825 paketa da bi popunio album... posto je cena jednog paketa oko 0.5 evra, znaci treba ti oko 4 glave da bi popunio "na seljaka"...ali draz je u menjanju... U realnosti sigurno vise... ne secam se da sam popunjavao album, a da nije bilo nekih koski od slicica koje su svima falile... kao veliki fan Panini World Cupa, prvi sam popunio Italiju 1990, pre par godina sam kupovao od kolekcionara one starije albume, i evropska i svetska prvenstva, tako da imam bogatu kolekciju... Ovaj zadnji sam popunjavao sa bratancem, falio nam je neki mamlaz iz Hondurasa, broj 400... jedva smo ga nasli...  Cela zajebancija je kostala oko 150 evra...
_________________
Pokaj se Grobi! Mali korak za tebe, veliki za Srpstvo!
|
|
| Vrh |
|
 |
|
Leonardo Da Vinci
|
Naslov: Re: Matematika  Postano: Postano: 04 lip 2014, 00:46 |
|
Pridružen/a: 03 ruj 2009, 01:51
Postovi: 798
|
Evo sad dva problema od mene. 1. Teorija brojeva (težina: easy to moderate) Koliko nula se nalazi na kraju broja 100! (100 faktorijela)? 2. Još jedan "Nemogući zadatak". (težina: extreme brain torture) Slijepi prosjak (bivši matematičar) prosi sjedeći na ulici i ljudi mu bacaju novčiće. Osluškuje i broji novčiće koji padaju oko njega. Kada se skupi 100 novčića razasutih oko njega, on zamoli jednog prolaznika da izbroji koliko novčića je okrenuto na pismo a koliko na glavu. Prolaznik mu kaže da "16 je okrenuto na glavu a ostali na pismo". Nakon par minuta prosjak razdvoji novčiće u dvije nejednake hrpe. U obje hrpe je bio isti broj glava! Kako je to napravio? Prosjak prstima (niti na bilo koji drugi način) ne može osjetiti detalje na površini novčića i ne osjeti razliku između pisma i glave, i ne postoji način da ikako sazna koji novčić je kako okrenut. Međutim može ih prevrtati po svojoj volji. Napomena: Kao što ste već navikli, kod mene nema nikakvog varanja i rješenja tipa "osam nos ti posran"  . Sva rješenja zaista postoje i razumna su.
|
|
| Vrh |
|
 |
|
Leonardo Da Vinci
|
Naslov: Re: Matematika  Postano: Postano: 04 lip 2014, 03:17 |
|
Pridružen/a: 03 ruj 2009, 01:51
Postovi: 798
|
DzoniBG je napisao/la: Kada imamo totalno prazan album, verovatnoca da ce prva slicica biti ona koju nemamo je 100%... vec druga slajba ima sansu (638/639)x100%...treca (637/639)x100%...itd...
Treća sličica ima veću šansu od 637/639, jer postoji šansa da je već druga duplikat. Ako je druga duplikat treća ima šansu 638/639. Zbrajanjem (?) tog gore niza nećeš dobit N*lnN. To gore je aritmetički red: 639/639+638/639+6...+1/639 = (N+1)/2 što iznosi samo 320. Kakogod, N*lnN jest približno točno rješenje na pitanje "Koliko "otprilike" treba kupiti da bi se popunio cijeli album". Pri tom treba razjasniti što znači "otprilike". Nikad ne možeš biti siguran da će određeni broj kupljenih sličica biti dovoljan, ako si jako nesretan niti jedan broj paketa ti neće biti dovoljan  , ali se može govoriti u vjerojatnostima. Može se postaviti pitanje "Koliko sličica moram kupiti da bi bila veća šansa da mi je album skroz popunjen, nego da nije"? odnosno koliko moraš kupiti da imaš preko 50% šanse da ti se popuni. Iz ovog izraza možeš dobiti koliko trebaš kupiti da ti fali sve osim jedne: f(n)=N[1-exp(-n/N)] Stavljanjem N-1 na lijevu stranu i logaritmiranjem dobijaš n=N*lnN. Ako probaš stavit n=N dobijaš naravno n=beskonačno. Znači N*lnN treba da fali u prosjeku samo jedna. E sad ako želiš da imaš sve osim jedne plus da ta zadnja ima šansu 50% da bude popunjena, onda treba zahtijevati da je očekivani broj popunjenih 638.5, odnosno na lijevu stranu uvrstiti N-1/2 ("fali pola sličice", što se može interpretirati kao šansa od bar 50% da je zadnja popunjena). Uvrštavanjem N-1/2 na lijevu stranu i logaritmiranjem dobija se da je potrebno kupiti: n=N*ln(2N)=4571 Dosta blizu ovome što si napisao.
|
|
| Vrh |
|
 |
|
DzoniBG
|
Naslov: Re: Matematika  Postano: Postano: 04 lip 2014, 11:21 |
|
Pridružen/a: 28 sij 2010, 18:54
Postovi: 13005
|
Leonardo Da Vinci je napisao/la: Evo sad dva problema od mene.
1. Teorija brojeva (težina: easy to moderate)
Koliko nula se nalazi na kraju broja 100! (100 faktorijela)?
Legao sam sa ovim problemom u mislima... nije bas easy, pre bi rekao moderate  Prvi osecaj je da se radi o astronomskoj brojki koju ne moze da ti izbaci digitron... znaci mora da mu se "doaka" iza ledja... Ideja je da vidimo koji su to brojevi koji kad se pomnoze sa drugim daju nulu na kraju... Imamo umnozak desetica, od kojih ce svaki dati bar jednu nulu...od 10 do 90...imamo stoju na kraju koja daje dve nulice... to je vec 11 nula na kraju... ako mnozimo 2 sa 50, odatle dobijamo jos jednu nulu...znaci to je 12-ta nula... Sad da prebrojimo petice... 5, 15, 25...95... nek svaku mnozimo sa brojem pre toga, 5 sa 4, 15 sa 14.... od svakog umnoska uberemo jos jednu nulu... to je ukupno 22 nule... imamo jos dve, kod umnozaka 24x25 i 74x75... Ako uzmemo u obzir da su umnosci brojeva koji se zavrsavaju sa 3, 7 i 9 skart... moj je odgovor je ukupno 24 nule na kraju ove dzombe od broja...
_________________
Pokaj se Grobi! Mali korak za tebe, veliki za Srpstvo!
|
|
| Vrh |
|
 |
|
DzoniBG
|
Naslov: Re: Matematika  Postano: Postano: 04 lip 2014, 11:28 |
|
Pridružen/a: 28 sij 2010, 18:54
Postovi: 13005
|
Leonardo Da Vinci je napisao/la:
Dosta blizu ovome što si napisao.
Slazem se... zato sam i rekao gore u objasnjenju da je ona formula ustvari aproksimacija... Dao si detaljno obrazlozenje kako se gomila mala greska... Radi se o prosecnom broju slicica koji treba kupiti da bi se popunio album... granicni slucajevi su da neko kupi 640 slicica i odmah popuni album, a neki mucenik kupuje desetine hiljada, i ne uspeva da popuni... u limesu do beskonacnosti... Sta rade ljudi u praksi...kupe kutiju od 100 paketa, to je 500 slicica... minimalan je broj duplikata, do pedesetak max... i onda im fali jos oko 200 da popune... ja to nikad nisam radio, trulo je da ti drugi dan album bude vec solidno popunjen... treba malo uzivati u tome...
_________________
Pokaj se Grobi! Mali korak za tebe, veliki za Srpstvo!
|
|
| Vrh |
|
 |
|
Ministry of Sound
|
Naslov: Re: Matematika  Postano: Postano: 04 lip 2014, 14:33 |
|
Pridružen/a: 03 svi 2009, 09:25
Postovi: 43757
Lokacija: Folklorni Jugoslaven, praktični Hrvat
|
Dečki, zahvaljujem na odgovorima, no meni a vjerujem i mnogima mozak eksplodira kada se krene u logove i slična apstraktna područja matematike. Najviše zbog sebe, a i ostalih, sam matematiku morao maksimalno pojednostaviti i sve svoditi na nekakvu "seljačku logiku". Pri tome je Excel nevjerojatan resurs. Evo screenshota, mog objašnjenja, koje je moja stara skontala za par sekundi. Dakle, nisam screenshotao cijeli niz od 0 do 639, nego samo početak i kraj. Ovim mojin načinom sam dogurao do 4496.22 kupljenih sličica potrebnih za punjenje albuma. Prva četiri reda su mislim jasna (broj popunjenih, ukupan broj sličica u albumu, šansa da će sljedeća kupljena sličica biti duplikat, šansa da sljedeća kupljena sličica neće biti duplikat). Ovaj red sa naslovom "Compensation" određuje koliko sličica morate kupiti kako bi popunili sličicu, i kompenzirali za mogućnost duplikata (1/chance of no duplicate). Zadnje dvije su ukupan broj kupljenih sličica i ukupan broj duplikata. Sa obzirom da neću postaviti cijelu datoteku, evo samo statistika za skupljače koliko duplih mogu očekivati: Od 0-100: 9 duplikata od 100-200: dodatnih 31 duplikata od 200-300: dodatnih 65 duplikata od 300-400: dodatnih 124 duplikata od 400-500: dodatnih 247 duplikata od 500-600: dodatnih 718 duplikata! od 600-639: dodatnih 2663 duplikata! Evidentno je da nakon 500-ak popunjenih (cirka 975 kupljenih), treba prestati bacati novac, ako ne i ranije. Na svu sreću, Panini nudi da ti pošalju 50 zadnjih kojih ti fale, po istoj cijeni kao i obične. 
_________________
sklon'se bona Zineta sa penđera, vidiš da te vlasi oćima kurišu

|
|
| Vrh |
|
 |
|
Mar-kan
|
Naslov: Re: Matematika  Postano: Postano: 04 lip 2014, 14:48 |
|
Pridružen/a: 03 svi 2009, 15:45
Postovi: 33103
|
|
Naručiti kompletan popunjen album od Paninija.
|
|
| Vrh |
|
 |
|
Ministry of Sound
|
Naslov: Re: Matematika  Postano: Postano: 04 lip 2014, 14:54 |
|
Pridružen/a: 03 svi 2009, 09:25
Postovi: 43757
Lokacija: Folklorni Jugoslaven, praktični Hrvat
|
|
Svakako da je to najjeftinije, ali jebiga, i taj gušt kupovanja paketića i mijenjanje ima nekakvu vrijednost. Inače, nakon što smo odradili ovaj zadatak sam uvjeren da su Talijani rekli istinu kada kažu da ne postoje neke sličice koje je "nemoguće" dobiti. Kao što brojke pokazuju, kada se tebi čini da je nemoguće dobiti neku sličicu koja ti fali, to je samo manifestacija činjenice da si pri kraju (da bi dobio zadnjih 39 sličica, moraš kupiti cirka 2.700 sličica!). A da Panini nešto namješta, onda ne bi nudili opciju da ti prodaju zadnjih 50 koje ti fale, ili čak popunjen album.
_________________
sklon'se bona Zineta sa penđera, vidiš da te vlasi oćima kurišu

|
|
| Vrh |
|
 |
|
Mar-kan
|
Naslov: Re: Matematika  Postano: Postano: 04 lip 2014, 15:01 |
|
Pridružen/a: 03 svi 2009, 15:45
Postovi: 33103
|
Ministry of Sound je napisao/la: Svakako da je to najjeftinije, ali jebiga, i taj gušt kupovanja paketića i mijenjanje ima nekakvu vrijednost. Inače, nakon što smo odradili ovaj zadatak sam uvjeren da su Talijani rekli istinu kada kažu da ne postoje neke sličice koje je "nemoguće" dobiti. Kao što brojke pokazuju, kada se tebi čini da je nemoguće dobiti neku sličicu koja ti fali, to je samo manifestacija činjenice da si pri kraju (da bi dobio zadnjih 39 sličica, moraš kupiti cirka 2.700 sličica!). A da Panini nešto namješta, onda ne bi nudili opciju da ti prodaju zadnjih 50 koje ti fale, ili čak popunjen album. To je pola-cijelo matematika:-)Iza škole,pa svaki odmor udri te igre.
|
|
| Vrh |
|
 |
|
Ministry of Sound
|
Naslov: Re: Matematika  Postano: Postano: 04 lip 2014, 15:30 |
|
Pridružen/a: 03 svi 2009, 09:25
Postovi: 43757
Lokacija: Folklorni Jugoslaven, praktični Hrvat
|
|
Postoji magazin Popular Science, koji je zanimljiv i laicima jer dotiče i mnoge svakodnevne teme i potrebe, pa se pitam je li moguće i matematiku preformulirati i prezentirati na sličan način. Ovo o Panini-ju, sa obzirom na popularnost je dušu dalo za neki članak, koji bi, uvjeren sam bio pročitan nekoliko stotina tisuća puta na nekom jačem portalu (Index, Klix, B92). Vjerojatno ima i drugih područja gdje se matematika može približiti običnim ljudima (ali ne sa zagonetkama i trikovima).
_________________
sklon'se bona Zineta sa penđera, vidiš da te vlasi oćima kurišu

|
|
| Vrh |
|
 |
|
Leonardo Da Vinci
|
Naslov: Re: Matematika  Postano: Postano: 05 lip 2014, 10:27 |
|
Pridružen/a: 03 ruj 2009, 01:51
Postovi: 798
|
DzoniBG je napisao/la: Leonardo Da Vinci je napisao/la: Evo sad dva problema od mene.
1. Teorija brojeva (težina: easy to moderate)
Koliko nula se nalazi na kraju broja 100! (100 faktorijela)?
Legao sam sa ovim problemom u mislima... nije bas easy, pre bi rekao moderate  Prvi osecaj je da se radi o astronomskoj brojki koju ne moze da ti izbaci digitron... znaci mora da mu se "doaka" iza ledja... Ideja je da vidimo koji su to brojevi koji kad se pomnoze sa drugim daju nulu na kraju... Imamo umnozak desetica, od kojih ce svaki dati bar jednu nulu...od 10 do 90...imamo stoju na kraju koja daje dve nulice... to je vec 11 nula na kraju... ako mnozimo 2 sa 50, odatle dobijamo jos jednu nulu...znaci to je 12-ta nula... Sad da prebrojimo petice... 5, 15, 25...95... nek svaku mnozimo sa brojem pre toga, 5 sa 4, 15 sa 14.... od svakog umnoska uberemo jos jednu nulu... to je ukupno 22 nule... imamo jos dve, kod umnozaka 24x25 i 74x75... Ako uzmemo u obzir da su umnosci brojeva koji se zavrsavaju sa 3, 7 i 9 skart... moj je odgovor je ukupno 24 nule na kraju ove dzombe od broja... 24 je točan odgovor. :)
|
|
| Vrh |
|
 |
|
DzoniBG
|
Naslov: Re: Matematika  Postano: Postano: 05 lip 2014, 11:41 |
|
Pridružen/a: 28 sij 2010, 18:54
Postovi: 13005
|
Ministry of Sound je napisao/la: Dečki, zahvaljujem na odgovorima, no meni a vjerujem i mnogima mozak eksplodira kada se krene u logove i slična apstraktna područja matematike. Najviše zbog sebe, a i ostalih, sam matematiku morao maksimalno pojednostaviti i sve svoditi na nekakvu "seljačku logiku". Pri tome je Excel nevjerojatan resurs. Evo screenshota, mog objašnjenja, koje je moja stara skontala za par sekundi. Dakle, nisam screenshotao cijeli niz od 0 do 639, nego samo početak i kraj. Ovim mojin načinom sam dogurao do 4496.22 kupljenih sličica potrebnih za punjenje albuma. Prva četiri reda su mislim jasna (broj popunjenih, ukupan broj sličica u albumu, šansa da će sljedeća kupljena sličica biti duplikat, šansa da sljedeća kupljena sličica neće biti duplikat). Ovaj red sa naslovom "Compensation" određuje koliko sličica morate kupiti kako bi popunili sličicu, i kompenzirali za mogućnost duplikata (1/chance of no duplicate). Zadnje dvije su ukupan broj kupljenih sličica i ukupan broj duplikata. Sa obzirom da neću postaviti cijelu datoteku, evo samo statistika za skupljače koliko duplih mogu očekivati: Od 0-100: 9 duplikata od 100-200: dodatnih 31 duplikata od 200-300: dodatnih 65 duplikata od 300-400: dodatnih 124 duplikata od 400-500: dodatnih 247 duplikata od 500-600: dodatnih 718 duplikata! od 600-639: dodatnih 2663 duplikata! Evidentno je da nakon 500-ak popunjenih (cirka 975 kupljenih), treba prestati bacati novac, ako ne i ranije. Na svu sreću, Panini nudi da ti pošalju 50 zadnjih kojih ti fale, po istoj cijeni kao i obične.  Dosao si do slicnih rezultata drugim putem... Lepo si ovo graficki predstavio... a najvazniji zakljucak je koliko je uzaludno kupovati slicice kad ti ostane malo na kraju...
_________________
Pokaj se Grobi! Mali korak za tebe, veliki za Srpstvo!
|
|
| Vrh |
|
 |
|
Ministry of Sound
|
Naslov: Re: Matematika  Postano: Postano: 04 srp 2014, 03:35 |
|
Pridružen/a: 03 svi 2009, 09:25
Postovi: 43757
Lokacija: Folklorni Jugoslaven, praktični Hrvat
|
|
Ajmo jedno (naizgled) lako pitanje. Ako imamo skupinu 50 aktivnih forumaša, kakve su šanse da među njima ima dvoje ljudi koji imaju isti rođendan?
_________________
sklon'se bona Zineta sa penđera, vidiš da te vlasi oćima kurišu

|
|
| Vrh |
|
 |
|
Kamov
|
Naslov: Re: Matematika  Postano: Postano: 04 srp 2014, 10:38 |
|
Pridružen/a: 23 svi 2014, 03:07
Postovi: 745
Lokacija: Planet Zemlja
|
Ministry of Sound je napisao/la: Ajmo jedno (naizgled) lako pitanje. Ako imamo skupinu 50 aktivnih forumaša, kakve su šanse da među njima ima dvoje ljudi koji imaju isti rođendan? Šanse su oko 97%
_________________
Došao je tiho i ušao u legendu
|
|
| Vrh |
|
 |
|
Ministry of Sound
|
Naslov: Re: Matematika  Postano: Postano: 09 srp 2014, 09:06 |
|
Pridružen/a: 03 svi 2009, 09:25
Postovi: 43757
Lokacija: Folklorni Jugoslaven, praktični Hrvat
|
Kamov je napisao/la: Ministry of Sound je napisao/la: Ajmo jedno (naizgled) lako pitanje. Ako imamo skupinu 50 aktivnih forumaša, kakve su šanse da među njima ima dvoje ljudi koji imaju isti rođendan? Šanse su oko 97% Točno, čekao sam da vidim hoće li se još netko javiti. Većina dijele broj ljudi sa brojem dana u godini (50/365=13.7%), no to ne uzima u obzir sve moguće parove. U skupini 50 ljudi imaš 1,225 mogućih parova (50*49/2). Vjerojatnoća da samo dvije osobe ne dijele isti rođendan je 364/365 = 99.73% Za tri osobe je (364/365)^3= 99.18% Za 50 osoba je (364/265)^1225 = 3.47%, odnosno vjerojatnoća od 100%-3.47%=96.53% da dvije osobe imaju isti rođendan. Za vjerojatnoću od 50% je dovoljno samo 23 ljudi.
_________________
sklon'se bona Zineta sa penđera, vidiš da te vlasi oćima kurišu

|
|
| Vrh |
|
 |
|
Leonardo Da Vinci
|
Naslov: Re: Matematika  Postano: Postano: 08 tra 2015, 07:07 |
|
Pridružen/a: 03 ruj 2009, 01:51
Postovi: 798
|
|
Ministar igra pikado i ima 3 strelice u ruci.
Baci prvu strelicu, a zatim baci i drugu.
Druga strelica je zavrsila dalje od centra nego prva.
Sada se sprema baciti i trecu strelicu.
Kolika je vjerojatnost da ce treca strelica, kada ju baci, zavrsiti dalje od centra nego prva strelica?
Kod svakog gadjanja, Ministar uvijek pokusava pogoditi sto blize centru i uvijek se maksimalno koncentrira (da sve od sebe).
|
|
| Vrh |
|
 |
|
Leonardo Da Vinci
|
Naslov: Re: Matematika  Postano: Postano: 08 tra 2015, 07:09 |
|
Pridružen/a: 03 ruj 2009, 01:51
Postovi: 798
|
Onaj tko je zbunjen zadatkom ili misli da se "ne moze izracunati" moze probati eksperimentirati ako ima kod kuce pikado. 
|
|
| Vrh |
|
 |
|
korrisnik
|
Naslov: Re: Matematika  Postano: Postano: 08 tra 2015, 19:13 |
|
Pridružen/a: 18 sij 2014, 17:10
Postovi: 15079
Lokacija: Pod kraljevskim Srebrn'kom
|
Leonardo Da Vinci je napisao/la: Onaj tko je zbunjen zadatkom ili misli da se "ne moze izracunati" moze probati eksperimentirati ako ima kod kuce pikado.  Ministar maša cijelo pikado.
_________________
Dušom i krvlju iskupit ćemo te, o Al-Aksa!
Bi ruh bi dam nafdika ya Aqsa” By our souls, by our blood, all for you oh Al-Aqsa
|
|
| Vrh |
|
 |
|
DzoniBG
|
Naslov: Re: Matematika  Postano: Postano: 08 tra 2015, 21:41 |
|
Pridružen/a: 28 sij 2010, 18:54
Postovi: 13005
|
Leonardo Da Vinci je napisao/la: Ministar igra pikado i ima 3 strelice u ruci.
Baci prvu strelicu, a zatim baci i drugu.
Druga strelica je zavrsila dalje od centra nego prva.
Sada se sprema baciti i trecu strelicu.
Kolika je vjerojatnost da ce treca strelica, kada ju baci, zavrsiti dalje od centra nego prva strelica?
Kod svakog gadjanja, Ministar uvijek pokusava pogoditi sto blize centru i uvijek se maksimalno koncentrira (da sve od sebe). Trebalo mi je dobrih 10-15 minuta da izadjem iz apsurdnosti ovako postavljenog zadatka, i potrazim logicni odgovor... Uzimajuci u obzir aproksimaciju da je svaki od 3 pokusaja potpuno nezavistan, verovatnoca da jedan do tri hica bude najbolji je 33.3%... treci hitac, kao i prva dva, da bi bio najbolji ima sansu samo 1/3...a posto se trazi da treci ne bude najbolji, tj da bude ili drugi ili treci po blizini centru, verovatnoca za takav ishod je 66%... Koliko je ovo gruba aproksimacija realne igre, znaju samo oni koji su igrali   Pravi pikado je ovakav... retko kad se cilja sam centar, "bull's eye" koji nosi 50 poena, "bull" koji nosi 25 poena... vec se na pocetku partije gadja gornje polje koje nosi 20 poena, i pokusava se pogoditi "triple ring", koji donosi 20x3=60 poena, to je najvrednije polje u igri...ako se i ne pogodi, vec ode gore ili dole, imas najmanje 20 poena(40 ako pogodis double ring). Sto se blizis cilju, vise kalkulises koje ces polje gadjati, treba na kraju u zbiru da imas tacno 301 ili 501, ako prebacis te brojeve, ponistavaju ti se poeni iz zadnjeg kruga bacanja... Realno bacanje strelica nikako ne moze biti nezavisno, da prvo ne utice na drugo, a drugo na trece... em sto stoje vec dve strelice na tabli pre bacanja trece, pa moras voditi racuna da njih ne pogodis, em sam pritisak nametnut u vezi dal su prva dva bila dobra hica ili ne, misao sta su rivali uradili ili ce uraditi, samopouzdanje ili manjak njega...koliko si uopste vest bacac, to pravi manje ili vece varijacije u krivi raspodele... pocetnici mogu da pogode sam centar, pa sledeca dva da ne pogode tablu, dok se pro igracima to ne moze desiti... Osim fizicke vestine, bacanje strelica je ozbiljna mentalna disciplina...
_________________
Pokaj se Grobi! Mali korak za tebe, veliki za Srpstvo!
|
|
| Vrh |
|
 |
Online |
Trenutno korisnika/ca: / i 9 gostiju. |
|
Ne možeš započinjati nove teme.
Ne možeš odgovarati na postove.
Ne možeš uređivati svoje postove.
Ne možeš izbrisati svoje postove.
Ne možeš postati privitke.
|
|
|





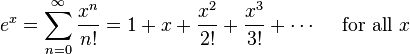
 . Sva rješenja zaista postoje i razumna su.
. Sva rješenja zaista postoje i razumna su.


